Diagonalen im n-Eck
Um Beweistechniken zu erlernen, beginnt man mit einfachen Beispielen.
Wir betrachten hier die Gleichung für die Anzahl der Diagonalen im n-Eck.
Der günstige Fall
Hat man eine Formelsammlung zur Hand, findet man für n >= 3 für die Anzahl d(n) der
Diagonalen folgende Gleichung
d(n) = n*(n-3)/2 (für n >= 3)
Wie kann man das sehen?
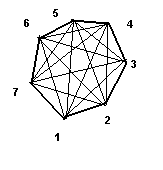 Beim 7-Eck gehen von Ecke 1 genau 7-3 Diagonalen aus.
Beim 7-Eck gehen von Ecke 1 genau 7-3 Diagonalen aus.
(Zur Ecke selbst und zu den beiden benachbarten Ecken führt keine Diagonale.)
Von jeder Ecke gehen gleich viele Diagonalen aus.
Das 7-Eck hat 7 Ecken. Jede Diagonale gehört zu genau 2 Ecken.
Somit ist 7*(7-3) die doppelte Anzahl der Diagonalen.
Diese Argumentation überträgt sich direkt auf das n-Eck, (falls n >= 3).
Der ungünstige Fall
Sie sitzen in einem Klassenzimmer, einem Seminarraum oder Zuhause und sollen eine
Gleichung für die Anzahl der Diagonalen im n-Eck aufstellen.
Eine Formelsammlung mit der fertigen Gleichung haben Sie nicht zur Hand.
Als erstes empfielt es sich einen Überblick für kleine n zu gewinnen.
| n = |
3 |
4 |
5 |
6 |
| |
 |
 |
 |
 |
| d(n) = |
0 |
2 |
5 |
9 |
Betrachten wir folgendes Bild
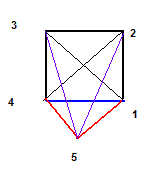 Wie ergibt sich die Diagonalenzahl des (n+1)-Ecks aus der des n-Ecks?
Wie ergibt sich die Diagonalenzahl des (n+1)-Ecks aus der des n-Ecks?
Wir fügen zum n-Eck eine weiter Ecke hinzu und verbinden sie mit den
Eckpunkten einer Seite. Diese Seite wird dann zu einer Diagonalen.
Die restlichen Eckpunkte des n-Ecks, das sind n-2, sind die Endpunkte weiterer Diagonalen.
Es kommen also n-1 Diagonalen hinzu.
Wir haben eine Rekursion gefunden:
d(3) = 0
d(n+1) = d(n) + (n-1) , für n >= 3
Finden der Gleichung
Aus den Werten des oben angegebenen Überblicks oder an der Rekursion sieht man,
dass d(n) nicht linear von n abhängt.
Wir versuchen ein Polynom 2-ten Grades als Ansatz:
d(n) = An2 + Bn + C
Wir setzen nacheinander n = 3, 4 und 5 ein und erhalten folgendes Gleichungssystem:
| I. |
d(3) |
= |
9A + 3B + C |
= |
0 |
| II. |
d(4) |
= |
16A + 4B + C |
= |
2 |
| III. |
d(5) |
= |
25A + 5B + C |
= |
5 |
III*. = III. - II. und II*. = II. - I. und anschließend
III**. = III*. - II*. führt zu
| I. |
9A + 3B + C |
= |
0 |
| II**. |
7A + B |
= |
2 |
| III**. |
2A |
= |
1 |
mit der Lösung:
A = 1/2 , B = -3/2 , C = 0
Damit erhalten wir:
d(n) = 1/2n2 - 3/2n
Ausklammern von n :
d(n) = n*(n-3)/2
Testen der Gleichung an n = 6 und n = 7 lässt uns vermuten, die richtige Gleichung gefunden zu haben.
Ist das schon ein Beweis?
Nein!
Induktionsbeweis
Das Prinzip der vollständigen Induktion wird in der Literatur in verschiedenen Formulierungen angegeben.
Wir verwenden hier:
"Gilt eine Aussage für eine natürliche Zahl n0 und
folgt für alle n >= n0 die Gültigkeit der Aussage für n+1 aus der Gültigkeit für n,
dann gilt diese Aussage für alle n >= n0 ."
Hiermit und mit der oben gefundenen Rekursion lässt sich die Gleichung für d(n) beweisen.
Induktionsanfang:
n0 = 3
0 = d(3) = 3*(3-3)/2
Induktionsschritt:
Sei n >= 3 und es gelte d(n) = n*(n-3)/2
Wir zeigen unter Verwendung der Rekursion, dass dann auch d(n+1) = (n+1)*((n+1)-3)/2 gilt.
d(n+1) = d(n) + (n-1)
= n*(n-3)/2 + (n-1)
= n*(n-3)/2 + (2n-2)/2
= (n2 - 3n + 2n - 2)/2
= (n2 + 2n + 1 - 3n- 3)/2
= ((n+1)2 - 3*(n+1))/2
= (n+1)*((n+1) - 3)/2
Induktionsschluss:
Die Gleichung ist für alle n >= 3 richtig.