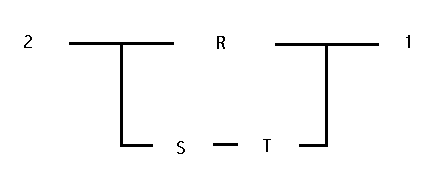
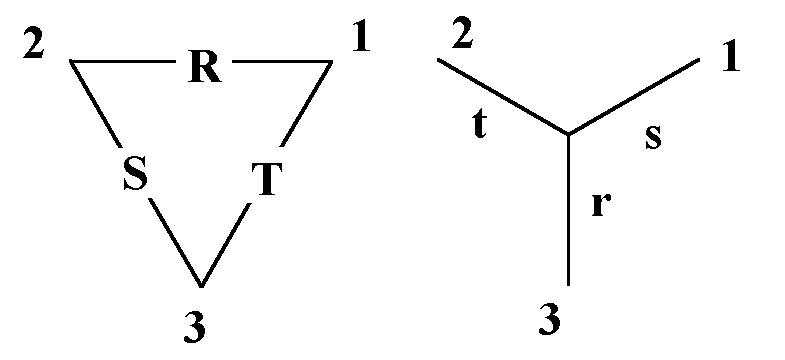
Drei Widerstände R, S, T in Dreieckschaltung können bekanntlich durch eine äquivalente Stern-Schaltung mit den
Widerständen r, s, t ersetzt werden.
Die Berechnungsgleichungen für r, s, t findet man in jeder guten Formelsammlung.
Der Vollständigkeit halber folgt die Herleitung.
Im Dreieck gilt für den Widerstand zwischen 1 und 2
(R-1 +(S+T)-1)-1 = (RS+RT) / (R+S+T)

Der Widerstand zwischen 1 und 2 ist im Stern s + t
Die Wiederstände zwischen 2 und 3 sowie zwischen 3 und 1 erhält man wegen der Symmetrie durch Austauschen
der Buchstaben.
Somit ergibt sich das folgende Gleichungssystem für r, s, t :
| r | s | t | |
| 0 | 1 | 1 | (RS+RT)/(R+S+T) |
| 1 | 0 | 1 | (ST+SR)/(R+S+T) |
| 1 | 1 | 0 | (TR+TS)/(R+S+T) |
Nach Auflösung erhält man die bekannten Gleichungen für r, s und t :
| ( 1 ) | r = S*T / (R+S+T) |
| ( 2 ) | s = T*R / (R+S+T) |
| ( 3 ) | t = R*S / (R+S+T) |
Das Umkehrproblem, aus gegebenen Werten r, s, t der Sternschaltung eine äquivalente Dreieckschaltung zu berechnen,
läßt sich hieraus wie folgt lösen.
Durch paarweise Division der oben angegebenen Bestimmungsgleichungen für r, s, t erhält man:
| ( * ) | r/s = S/R | s/t = T/S | t/r = R/T | bzw. |
| ( ** ) | S = r*R/s | T = s*S/t | R = t*T/r | T = r*R/t |
Für das Folgende setzen wir Σ := R+S+T
Ersetzt man in r = S*T / Σ S und T durch Ausdrücke in R, so erhält man:
| r = r*R*r*R / s*t*Σ |
Nach Umformung und Ausnützen der Symmetrie entstehen die folgenden drei Gleichungen:
| I. | s*t*Σ =r*R2 |
| II. | r*s*Σ =t*T2 |
| III. | t*r*Σ =s*S2 |
Aus den Gleichungen ( 1 ),( 2 ),( 3 ) und ( ** ) gewinnt man:
| IV. | r*R = s*S = t*T = R*S*T / Σ |
Aus den Gleichungen I., II., III. und IV. erhält man:
| s*t*Σ = R*R*S*T / Σ |
| r*s*Σ = T*R*S*T / Σ |
| t*r*Σ = S*R*S*T / Σ |
Zusammenaddieren dieser letzten drei Gleichungen ergibt mit Gleichung IV:
Auflösen nach S und Ausnutzen der Symmetrie liefert die gesuchten Gleichungen:
| S = (s*t + r*s + t*r) / s |
| R = (s*t + r*s + t*r) / r |
| T = (s*t + r*s + t*r) / t |